854 . 巴乙己的暸望塔
TopCoder
Tags
Description
最近，王董買了一個海岸，IOICamp 2225 的總召巴乙己準備要借用這個海岸，來當作 IOICamp 2225 的其中一項活動──皮卡丘打排球大賽的活動場地。巴乙己為了好好觀賞這項 IOICamp 之中最精彩的活動，他建造了一座暸望塔，並且打算在皮卡丘打排球大賽期間待在暸望塔上。
這個海岸的海岸線可以被視為一條直線，而暸望塔正好被建造在海岸線上，皮卡丘打排球大賽的所有活動都在海岸線上進行，所以巴乙己只關心海岸線和海岸線的上空，於是他決定把海岸線和暸望塔所在的平面畫在二維平面上，海岸線是平面上從 $(-10^ {8 \times 10^ 7}, 0)$ 到 $(10^ {8 \times 10^ 7}, 0)$ 的線段（這個海岸線很長！），暸望塔頂端在這個平面上的座標是 $(s_x,s_y)$。
在皮卡丘打排球大賽的前幾天，巴乙己發現海岸線上空出現了 $N$ 朵烏雲，其中第 $i$ 朵烏雲是在平面上的 $(x_{i,1},y_i)$ 到 $(x_{i,2},y_i)$ 這條線段，烏雲會擋住巴乙己的視線，使他看不見一部份的海岸線。正式地說，巴乙己能看見海岸線上的一個點 $(x,0)$，若 $(s_x,s_y)$ 到 $(x,0)$ 這條線段不和任何烏雲相交（在端點也不行）。
為了確保良好的觀賽體驗，請告訴巴乙己，他不能看見的海岸線長度有多長。
Input Format
第一行有三個整數 $N,s_x,s_y$，代表海岸線上空出現了 $N$ 朵烏雲，以及暸望塔頂端的座標是 $(s_x,s_y)$。
接下來有 $N$ 行，其中第 $i$ 行包含三個整數 $x_{i,1},x_{i,2},y_i$，代表第 $i$ 朵烏雲對應到線段 $(x_{i,1},y_i)$ 到 $(x_{i,2},y_i)$。
- $1 \leq N \leq 5 \times 10^ 5$
- $-10^ 9 \leq s_x \leq 10^ 9$
- $-10^ 9 \leq x_{i,1} < x_{i,2} \leq 10^ 9$
- $0 < y_i < s_y \leq 10^ 9$
Output Format
輸出一個浮點數，代表巴乙己看不見的海岸線長度。若你的答案與正確答案的相對或絕對誤差 $\leq 10^ {-6}$，就會被視為正確。正式地說，假設正確答案是 $a$、你的答案是 $b$，你的答案會被視為正確的條件是 $\frac{\lvert a-b \rvert}{\max(\lvert a \rvert, \lvert b \rvert, 1)} \leq 10^ {-6}$。
Sample Input 1
1 5 8
-7 -3 4
6 9 6
11 15 7
11 13 4
Sample Output 1
Sample Input 2
-6 0 6
-2 4 6
6 12 6
10 16 6
8 11 6
Sample Output 2
Hints
目前的 IOICamp 沒有皮卡丘打排球大賽。
以下為兩筆範例測試資料的示意圖，綠色點是暸望塔頂端所在的位置、灰色陰影是巴乙己看不見的區域：
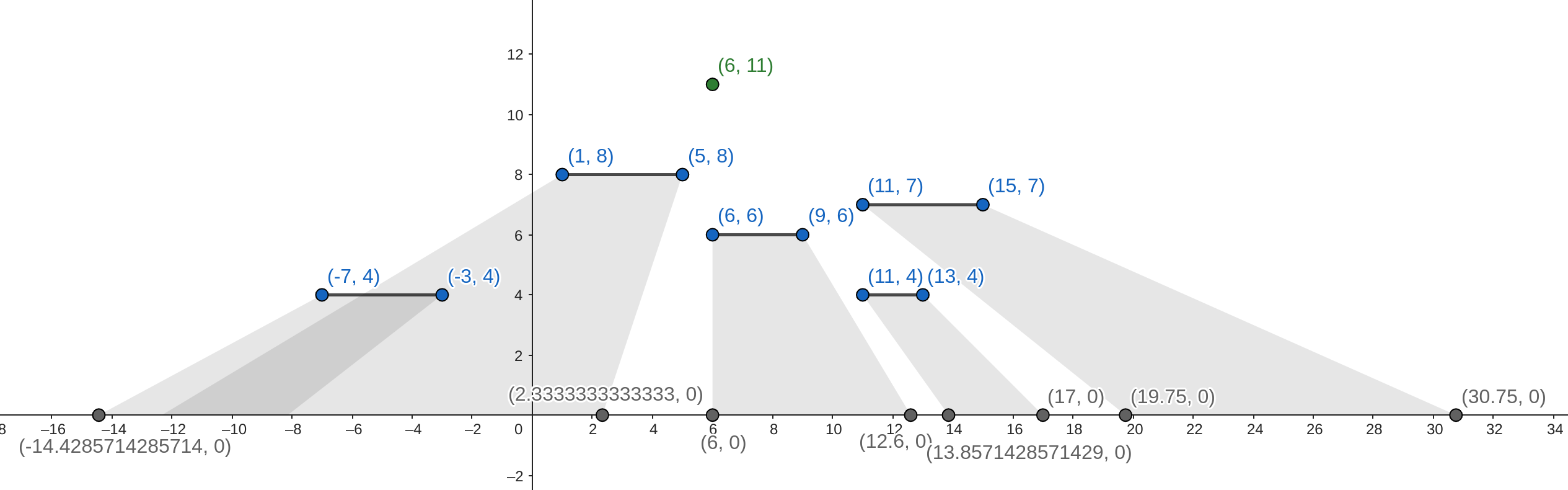
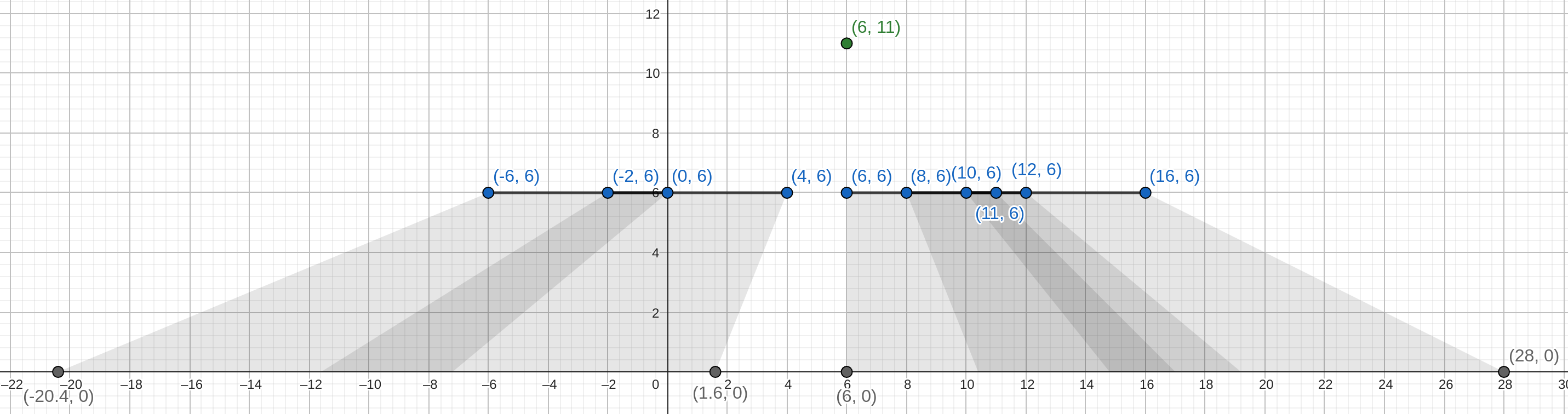
Problem Source
Subtasks
| No. | Testdata Range | Constraints | Score |
|---|---|---|---|
| 1 | 0~1 | 範例測資 | 0 |
| 2 | 2~5 | $N=1$ | 5 |
| 3 | 6~14 | 所有 $y_i$ 皆相同 | 30 |
| 4 | 2~25 | 無額外限制 | 65 |