574 . 小明的矩陣乘法

Submit
Status
Discussion / Solution
Ranklist
Back to Problems List

TopCoder

r

User's AC Ratio

100.0% (4/4)

Submission's AC Ratio

36.4% (4/11)

Tags

apcsc apcsc-2darray

Description

有一天小明與小華在教室裡上數學課

「矩陣的乘法吼，也可以用連加的符號以及矩陣元素 $a_{ij},b_{ij}$ 表示」老師在講台上口沫橫飛地講著。

「咦？這樣不就可以使用迴圈計算矩陣 $AB$ 的乘積了嗎！」小明興奮地回頭對小華說著，殊不知小華早已睡倒在桌上不省人事。

於是小明想請你幫他完成這個程式，這樣他才有時間叫小華起床。

  • 已知矩陣 $A$ 的大小為 $m\times n$，矩陣 $B$ 的大小為 $n\times p$。矩陣的乘積只有當 $A$ 的行數等於 $B$ 的列數時才有定義，此時相乘得到的矩陣 $AB$ 的大小為 $m\times p$。
  • 請實作一個程式，讀入二矩陣 $A,B$ 並輸出其相乘的結果。若矩陣 $A,B$ 的相乘沒有定義（即當 $A$ 的行數不等於 $B$ 的列數時）請輸出 no answer。

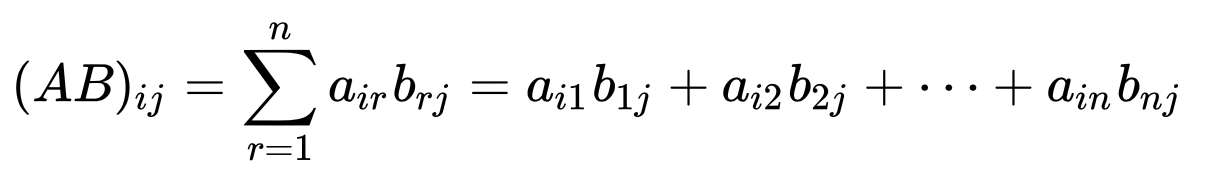
（圖片截自維基百科：https://zh.wikipedia.org/zh-tw/矩陣乘法）

Input Format

輸入的第一行包含四個正整數 $r_1,c_1,r_2,c_2(1\le r_1,c_1,r_2,c_2 \le 100)$，其中 $r_1,c_1$ 代表矩陣 $A$ 的列數與行數、$r_2,c_2$ 代表矩陣 $B$ 的列數與行數。接下來的 $r_1$ 行每行有 $c_1$ 個整數，代表一個 $r_1\times c_1$ 的矩陣 $A$。再來的 $r_2$ 行每行有 $c_2$ 個數字，代表一個 $r_2\times c_2$ 的矩陣 $B$。所有 $A,B$ 的矩陣元素皆滿足 $-1000\le a_{ij},b_{ij}\le 1000$。

Output Format

若矩陣 $A,B$ 的乘法沒有定義（即 $c_1\neq r_2$），請輸出 no answer 於一行。

否則請輸出 $r_1$ 行，每行有 $c_2$ 個整數（第 $i$ 行第 $j$ 個代表元素 $(AB)_{ij}$，$1\le i\le r_1,1\le j\le c_2$），代表矩陣 $A,B$ 相乘的結果 $AB$（大小為 $r_1\times c_2$）。

Sample Input 1

2 2 2 3
1 0
3 1
0 1 3
-1 2 2

Sample Output 1

0 1 3
-1 5 11

Sample Input 2

2 1 2 2
1
1
1 2
3 4

Sample Output 2

no answer

Hints

Problem Source

Subtasks

No. Testdata Range Constraints Score
1 0~1 範例測資 0
2 0~11 無額外限制 100

Testdata and Limits

No. Time Limit (ms) Memory Limit (VSS, KiB) Output Limit (KiB) Subtasks
0 1000 524288 65536 1 2
1 1000 524288 65536 1 2
2 1000 524288 65536 2
3 1000 524288 65536 2
4 1000 524288 65536 2
5 1000 524288 65536 2
6 1000 524288 65536 2
7 1000 524288 65536 2
8 1000 524288 65536 2
9 1000 524288 65536 2
10 1000 524288 65536 2
11 1000 524288 65536 2
Submit
Back to Top