IOIC 2025 題目已公開! 連結
程式解題社網站 程式解題社網站上線了!
Judge 將在 3/7~3/8 進行系統更新 可能會有不穩定的情況 敬請見諒
566 . 棒球遊戲
TopCoder
Tags
Description
謙謙最近迷上棒球,他想自己寫一個簡化的棒球遊戲計分程式。這個程式會讀入球隊中每位球員的打擊結果,然後計算出球隊的得分。
這是個簡化版的模擬,假設擊球員的打擊結果只有以下情況:
- 安打:以
1B、2B、3B和HR分別代表一壘打、二壘打、三壘打和全(四)壘打。 - 出局:以
FO、GO和SO表示。
這個簡化版的規則如下:
- 球場上有四個壘包,稱為本壘、一壘、二壘和三壘。
- 站在本壘握著球棒打球的稱為「擊球員」,站在另外三個壘包的稱為「跑壘員」。
- 當擊球員的打擊結果為「安打」時,場上球員(擊球員與跑壘員)可以移動;結果為「出局」時,跑壘員不動,擊球員離場,換下一位擊球員。
- 球隊總共有九位球員,依序排列。比賽開始由第 $1$ 位開始打擊,當第 $i$ 位球員打擊完畢後,由第 $(i+1)$ 位球員擔任擊球員。當第九位球員完畢後,則輪回第一位球員。
- 當打出 $K$ 壘打時,場上球員(擊球員和跑壘員)會前進 $K$ 個壘包。從本壘前進一個壘包會移動到一壘、接著是二壘、三壘,最後回到本壘。
- 每位球員回到本壘時可得 $1$ 分。
- 每達到三個出局數時,一、二和三壘就會清空(跑壘員都得離開),重新開始。
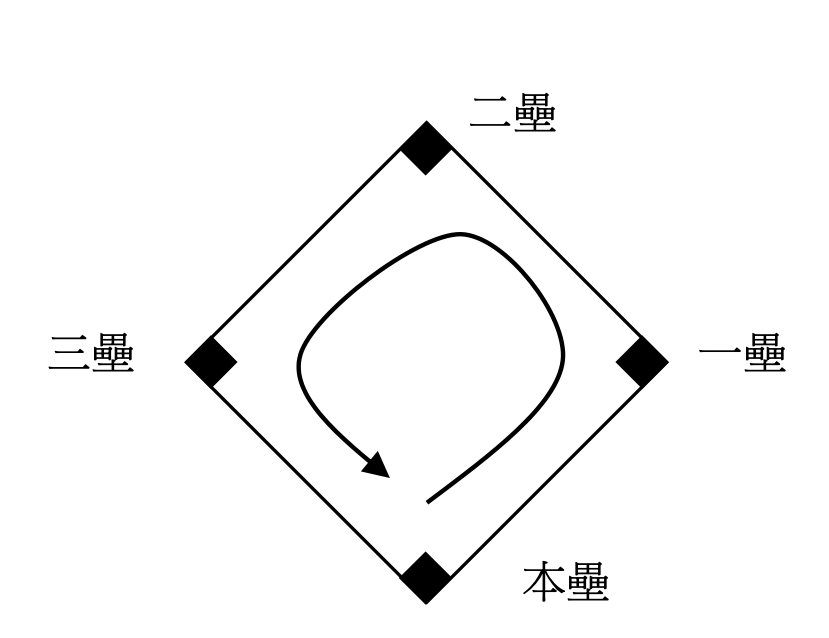
請寫出具備這樣功能的程式,計算球隊的總得分。
範例輸出一說明:
1B:一壘有跑壘員。
1B:一、二壘有跑壘員。
SO:一、二壘有跑壘員,一出局。
FO:一、二壘有跑壘員,兩出局。
1B:一、二、三壘有跑壘員,兩出局。
GO:一、二、三壘有跑壘員,三出局。
達到第三個出局數時,一、二、三壘均有跑壘員,但無法得分。因為 $b=3$,代表三個出局就結束比賽,因此得到 $0$ 分。
範例輸出二說明:
接續範例一,達到第三個出局數時未得分,壘上清空。
1B:一壘有跑壘員。
SO:一壘有跑壘員,一出局。
3B:三壘有跑壘員,一出局,得一分。
1B:一壘有跑壘員,一出局,得兩分。
2B:二、三壘有跑壘員,一出局,得兩分。
HR:一出局,得五分。
FO:兩出局,得五分。
1B:一壘有跑壘員,兩出局,得五分。
GO:一壘有跑壘員,三出局,得五分。
因為 $b=6$,代表要計算的是累積六個出局時的得分,因此在前 $3$ 個出局數時得 $0$ 分,第 $4\sim6$ 個出局數得到 $5$ 分,因此總得分是 $0+5=5$ 分。
Input Format
每組測試資料固定有十行。
第一到九行,依照球員順序,每一行代表一位球員的打擊資訊。每一行開始有一個正整數 $a$,代表球員總共打了 $a$ 次。接下來有 $a$ 個字串(均為兩個字元),依序代表每次打擊的結果。資料之間均以一個空白字元隔開。球員的打擊資訊不會有錯誤也不會缺漏。
第十行有一個正整數 $b$,表示我們想要計算當總出局數累計到 $b$ 時,該球隊的得分。輸入的打擊資訊中至少包含 $b$ 個出局。
- $1\le a\le5$
- $1\le b\le27$
Output Format
計算在總計第 $b$ 個出局數發生時的總得分,並將此得分輸出於一行。
Sample Input 1
5 1B 1B FO GO 1B 5 1B 2B FO FO SO 4 SO HR SO 1B 4 FO FO FO HR 4 1B 1B 1B 1B 4 GO GO 3B GO 4 1B GO GO SO 4 SO GO 2B 2B 4 3B GO GO FO 3
Sample Output 1
0
Sample Input 2
5 1B 1B FO GO 1B 5 1B 2B FO FO SO 4 SO HR SO 1B 4 FO FO FO HR 4 1B 1B 1B 1B 4 GO GO 3B GO 4 1B GO GO SO 4 SO GO 2B 2B 4 3B GO GO FO 6
Sample Output 2
5
Hints
Problem Source
APCS 考古題
Subtasks
| No. | Testdata Range | Constraints | Score |
|---|---|---|---|
| 1 | 0~1 | 範例測資 | 0 |
| 2 | 2~6 | 打擊表現只有 HR 和 SO 兩種 | 20 |
| 3 | 7~11 | 安打表現只有 1B,而且 b 固定為 3 | 20 |
| 4 | 12~16 | b 固定為 3 | 20 |
| 5 | 0~21 | 無額外限制 | 40 |
